Python and R are the two most popular and widely used programming languages in the data science field. But which language among these two should you choose? Well, let’s compare both these programming languages based on different factors to find out who the winner is.
Purpose of Comparison:
- Which language is better for Data Science?
- Which language will give you a solution with less cumbersome code?
- Which language provides a better graphical display?
- Should you learn R or Python or Both?
- Is it necessary to learn both languages?
- Suppose you need a faster solution, should you go for Python or R?
And many more questions arrive in your mind. It’s an obvious question that comes in every beginner’s mind who is not aware of these things, or maybe lack knowledge or unable to do a comparison between these two languages.
So, take a seat back, because we are going on a journey of comparison of Python Vs R for Data Science. Both languages have their unique strengths and weaknesses. Both languages compare to each other from a data science and analytics perspective. Without any further chitchat, let’s dive into the comparison.
History of Python and R
Python was started by Guido Von Rossum. Inside the python network, he’s called a “benevolent dictator for life”, meaning that he keeps overseeing the python development method, making decisions as required.
Why the Name Python? Well, Guido van Rossum was reading the script of a popular BBC comedy series “Monty Python’s Flying Circus”. It was the late on-air 1970s. He wanted to select a name which unique, sort, and a little bit mysterious.
Thus he decided to pick out the name Python from “Monty Python’s Flying Circus” for their newly created programming language. The comedy series was inventive and well random. It talks about everything. Thus it’s miles sluggish and unpredictable, which made it very exciting.
R was designed by Ross Ihaka and Robert Gentleman in 1991.
R’s software environment was written primarily in C, FORTRAN, and R. It focuses on superior data analysis, statistical interpretation, and visualization tools. The closer you are to the data science and statistics field, the more you prefer R.
Why Use Python or R?
- Python is a widely-used general-purpose, high-level programming language that is used for data analysis. R also has much functionality for data analysis.
- Both are open-source tools. Anyone can use and change it. We can run anywhere and at any time.
- Both languages are very easy to learn and are beginner-friendly. You can choose either Python or R even if you don’t have any prior experience in coding.
- Code readability is an important feature in Python. It is designed to write clean code which can be easily read by any programmer. Python codes are easier to maintain but more robust than R.
- Both Python and R, are strongly but dynamically typed, functional, and interpreted.
- Both Python and R are highly extensible. R extensible algorithms are stronger to assist and sign up extra algorithms for SQL users and graphical interface users. Python can also be embedded in existing applications that require a programmable interface.
- R provides dynamic and interactive graphics with the help of additional packages. R is considered the best tool for making graphs and visualization compared to Python.
- Python is used by programmers that want to delve into data analysis or apply statistical techniques. But R is more preferable for Statistical analysis where Python provides just a general approach to data science.
- RStudio is the most used IDE for R. It includes a console, syntax-highlighting editor that helps direct code execution, in addition to tools for plotting, records, debugging, and workspace management. In evaluation to R, Python has no clear “winning” IDE. You have to look at IPython Notebook, Spyder, and Rodeo to see which one best fits your needs.
- Usually, engineers prefer Python as they can do many other things in other areas like Artificial Intelligence, Games, Hardware/Sensors/Robots, Desktop Applications.
Features of Python and R
Python has a robust ecosystem and it has a very clean and readable syntax so coding and debugging are much easier. Proper indentation helps in faster debugging.
Python is considered to be an ideal and good language for novice programmers. Due to its focus on readability and simplicity, the learning curve for Python is relatively low. Beginners can easily pick it up and keep going.
R has a rich ecosystem and it is very easy to use for solving statistical problems as statistical models can be written with only a few lines of code and displaying options are excellent. There is versatility in R because the same functionality can be written in several ways.
R has an extensive collection of complex formulas related to data analysis in CRAN (Comprehensive R Archive Network). So, all kinds of statistical tests and models are readily available and easily used. Also, users can contribute too. R has a steep learning curve at the start and after learning the basics, it is easy to progress and learn advanced concepts.
How Do Python & R Differ In Data Science Processes?
Let’s see how these two languages contribute regarding their use in the data pipeline, including processing:
- Data Collection
- Data Exploration
- Data Modelling
- Data Visualization
Differences in Data Collection
Python: For Data Collection, Python supports various data formats such as CSVs, JSON files, and even SQL files. Python can also allow you to extract data directly from the internet with the help of suitable libraries like Python Request Library, beautifulsoup.
R: Data can be imported from Excel, CSV, text files. Files built-in Minitab or in SPSS format can be converted into R data frames. Packages like dplyr, tidyr, and data.table are used to easily manipulate data. R is not much flexible to grab information from the internet. But many modern packages such as Rvest and magrittr are built recently for that purpose.
Differences in Data Exploration
Python: Python’s various libraries like Pandas and NumPy helps in analyzing the structure and unstructured data very easily. Pandas is responsible for holding a large amount of data, converting it into a data frame, filtering, sorting, and cleaning up the data. The statsmodels library is used to estimate statistical models, perform statistical tests and unit tests.
R was mainly built for statistical and numerical analysis of large data sets. So, it’s an obvious conclusion that you have many options for data exploration. You can perform probability distributions, apply a variety of statistical tests to your data, and use standard machine learning and data mining techniques. Also, R offers support of third-party libraries.
Differences in Data Modelling
Python: For Data Modelling, python provides various libraries that help you to achieve desired results in modeling. For, numerical modeling, Python provides the NumPy library. For scientific computing and calculation, it has SciPy. And for working with machine learning algorithms, it provides Scikit-learn.
R: Without any doubt, you can easily do statistical modeling efficiently with R. It provides so many packages that support specific analyses such as the Poisson distribution and mixtures of probability laws. For working on machine learning algorithms, the caret library is used.
Differences in Data Visualization
Python: You can use Matplotlib and Seaborn to generate basic graphs and charts from the data. These are the most commonly used Python libraries for data visualization.
R: R is used for advanced visualizations. R comes with built-in support for many standard graphs, even for more complex visualizations. R provides libraries, such as ggplot2, Plotly, and Lattice.
Advantages & Disadvantages of Python and R
Let’s look at some of the pros and cons of using Python and R for data science.
Advantages of Python
- Python is super easy to learn.
- Python provides simplicity and readability, which makes it a beginner-friendly language.
- Python has been made richer with the inclusion of several libraries that enhance its capabilities.
- Python is not a strictly object-oriented programming language. It is actually a multi-paradigm programming language. For example, In Java, you’d be required to create a separate class for printing ‘Hello World,’ whereas in Python you do not have to do so.
- Python community is a great strength of the language and will always be there for you. That’s because of the popularity of the language. You’ll not face any trouble in finding good tutorials and answers to your doubts. Python language has a huge fan base all across the world.
Check out this article to learn more about the advantages of Python.
Advantages of R
- R language provides more statistical support than Python.
- R has a huge community and the biggest number of statistical libraries and packages.
- R is a function-based language.
- Tidyverse makes data wrangling/cleaning more efficient.
- R generates the most beautiful visualizations and graphs.
Disadvantages of Python
- Python is slow in the execution of code. However, many Python packages have been optimized over the years and executed at a decent speed.
- Python language is a dynamically typed language that poses certain design restrictions. It needs rigorous testing and errors show up solely throughout the runtime.
- It has a limitation on database access.
Check out this article to learn about the disadvantages of Python in detail.
Disadvantages of R
- Sometimes, it is difficult to find the right package in R.
- If you write your code badly, then it takes an excessive amount of time to execute the code.
- R was created for statisticians. Thus, a beginner may find it hard to learn as things may be complex for them.
- R isn’t a popular language compared to Python.
- There are several dependencies between R libraries.
- R has fewer deep learning libraries and other frameworks compared to Python.
Trends and Visualization
1) Stack Overflow Trends:
Python trend is going high compared to R.
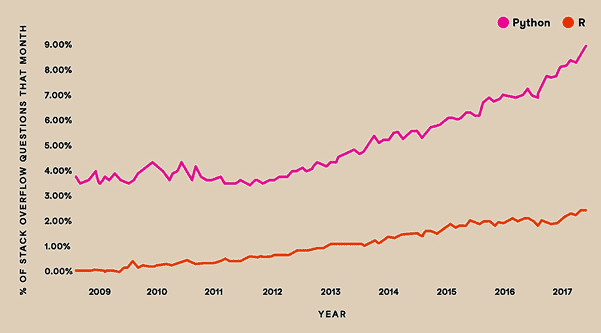
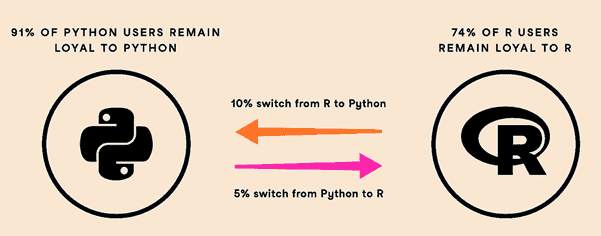
2) User-loyalty in Python vs R:
You can clearly observe that Python fans are much loyal compared to R fans. The switching rate from R to Python is twice that of Python to R.
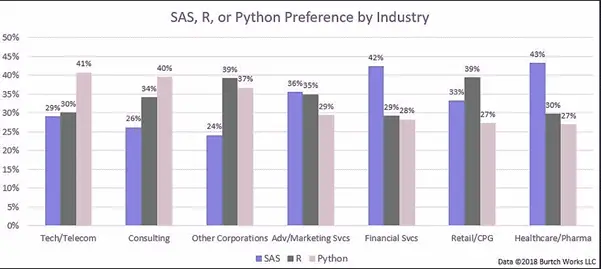
3) SAS, R or Python Preference by Industry:
Final Thoughts
Given below are some questions that can help you in choosing the right language for data science:
- What varieties of issues do you need to solve?
- Do you already know one of these languages? If no, what cost it will take to learn?
- What are the commonly used tools in your field? Do they give a worthwhile solution? What are the other available tools?
- What level of visualization do you require in your presentations?
- Are you an academic, research-oriented, or commercial professional?
Find answers to these questions and select the language of your choice. Happy coding!


What an amazing article comparing Python and R. Thanks for writing this, really helpful for me.
You’re welcome, I’m glad it helped you.